Doodle Insights #19: Logic Data Generation (feat. WFC made easy)

Generating things is easy. You just take a few random numbers, pick and change a few things based on these numbers, put them together somehow and boom you’ve generated something. You don’t even need a computer.

But sometimes you want to generate complex things and in particular: complex things that make sense. Coherent things are harder to generate than mere organized chaos of course, but it seems the difficulty would increase with the complexity of said coherant things. Or would it?

When making any Thing Generator, you can’t always only focus on the generated results. You’ll need to focus on the generation itself as well. The systems you make and/or use can be reworked and taken in new direction to achieve the goals you want to meet. And if your goal is to let your Coherent Thing Generator have expendable complexity, you betcha there’s a way.

Today we’re looking at different ways to generate logic constructions, where the complexity of those constructions has only a minimal impact on the bother to actually make it happen!

This Doodle is a demake of Orteil‘s Nested!

In this doodle, you can browse through the entire universe, infinitely. Everything is randomly generated. This is mainly possible through the use of a custom dictionary system and the use of seeds for the randomness!

The ‘logic’ here in this doodle is the organization of the data, its coherence. To simulate this coherence, I wrote a set of data, mapped with the use of table. The data refers to other parts of the data, for an ever-looping generation. Here’s an excerpt from it:

elements={
 [...]
 galaxy_cluster={
  poss={
   "galaxy"
  }
 },
 galaxy={
  always={
   "galactic_center"
  },
  poss={
   "arm"
  }
 },
 galactic_center={
  poss={
   "black_hole",
   "star_system",
   "asteroid_belt",
   "star",
   "twin_star"
  },
  rare={
   "nyan_cat"
  }
 },
 [...]

When generating an element’s content, we look up the name of that element in the table. If that element has an ‘always’ field, anything that’s set there we put in this element. Then if there’s a ‘poss’ field, we add a random number of ‘poss’ things, which are chosen at random. If there’s a ‘rare’ field, there’s a tiny chance that something in this field is added too.

This is a pretty simple system but it works really well. The limit of the generation is the size and complexity of your library of elements. This simple system is already enough to make something fun and to have fun yourself while making it.

But it is somewhat limited by the format of the data and by the simplistic generation algorithm. Putting things in arrays is easy enough but we could probably make something more comfortable. The array syntax takes space and the syntax errors you’ll get from missing commas might drive you to the edge of sanity. Aside from that, maybe you would like to set specific chances for some things to appear or not and maybe you’d like to have more control over the quantity of each type of thing in each element. Maybe you’d like to have randomly-generated elements!

We can do better!

This is not actually a Doodle! It’s my procjam entry from last year and you can check it out over there!

Kate Compton (@GalaxyKate)‘s Tracery is a javascript library that lets you create grammars by writing a lexicon of possibilities. Much like in the previous doodle, it works mostly with a lot of arrays of user-written data. But the result is very different. Here, we’re generating sentences.

Short or long, complex or even non-verbal, Tracery allows for any kind of sentence you’d like to see, with a lot of control over it, as you are the master of what the algorithm gets to say. In your library of possibilities, you can link any possibility to any other possibility, even to itself if you want to get recursive. Here’s how the syntax works:

{
 "origin":["[myPlace:#path#]#line#"],
 "line":[
       "#mood.capitalize# and #mood#, the #myPlace# was #mood# with #substance#",
       "#nearby.capitalize# #myPlace.a# #move.ed# through the #path#, filling me with #substance#"
 ],
 "nearby":["beyond the #path#", "far away", "ahead", "behind me"],
 "substance":["light", "mist", "shadow", "darkness", "brightness", "merriment"],
 "mood":["clear", "darkened", "blue", "shadowed", "illuminated", "warm", "summer-warmed"],
 "path":["stream", "brook", "path", "ravine", "forest", "fence", "stone wall"],
 "move":["twirl", "curl", "dance", "twine", "weave", "wander", "flow"]
}

generated results:
"Far away a stone wall wandered through the path, filling me with light"
"Blue and clear, the ravine was darkened with darkness"
"Blue and illuminated, the fence was illuminated with mist"

Example directly taken from tracery.io/editor. (and reduced a little, so it fits)

The gif above is my attempt at recreating the magic in Pico-8. It works but it’s very incomplete. The actual Tracery has a system of memory which lets you reuse some of the generated result later in the same generated result. It allows for actual novel generation – coherant novel generation!

It’s really powerful and it’s super easy to use. You can even use it to generate graphics by plugging it into some sort of graphical library. CheapBotsDoneQuick by George Buckenham (@v21) uses Tracery to let you create Tweetbots. It gave birth to some amazing bots out there. I made one a while ago and I really think you should give it a try too, because it is honestly a lot of fun!

Tracery let’s you achieve impressive complexity in its generated results and it is very easy to use and it lets you keep a lot of control over what’s being generated. But. That control does fade away as you get deeper and deeper in the complexity. You’ll get what you wanted to generate but you may also get some unwanted results which will require workarounds. Besides, even if it can generate graphics (and possibly a lot of other cool stuff), that actually seems somewhat less accessible and very much limited to the graphic interface you’ll be using. I haven’t tried it yet though, consider this as only a suspicion.

Still, Tracery really is wonderful stuff and you should check it out. However, it is limited to its first purpose of simulating grammar, even though that itself opens up a lot of possibilities; maybe what you want to make isn’t part of those possibilities. Let’s take a look at something else.

Can it get more logic-inclined than logic puzzles?

Sudoku generation is not really a versatile algorithm, it can’t do much else than sudokus, maybe of different sizes. But, sudoku generation is a really good first step towards the next technique we’ll see, so let’s study that first.

Generating sudokus is a lot easier than it may seem. All you need is a board solver – an algorithm that can read the board and solve it.

Just in case you don’t know what a sudoku is or how it works, here’s a definition from Merriam-Webster:

[A sudoku is] a puzzle in which missing numbers are to be filled into a 9 by 9 grid of squares which are subdivided into 3 by 3 boxes so that every row, every column, and every box contains the numbers 1 through 9.

(This next paragraph is important)

Classically, the way you solve a sudoku is that you take individual empty squares and consider they have a pool of 9 possibilities (the 9 numbers). Then you look at their line, column and box and, since no number should be seen twice on any line, column or box, all the numbers you see there should be removed from the pool of possibilities for the square.

The trick is of course to find the squares where the pool of possibilities can be reduced to one possibility, put that remaining value in the square and have that information on the board to reduce the possibilities of the other squares.

Maybe you already got that from the way I explained it, but this is very easily translatable to an algorithm!

First, the algorithm should have all the information that’s already on the board. Then, all the empty squares on the board should be set as dynamic arrays (aka lists) of 9 possibilities. Then, we read the entire initial board and remove possibilities from empty cases accordingly. Finally, we find the empty squares with only one remaining possibility and use the new information to remove possibilities in other empty squares. Repeat that last step until there’s no more empty square on the board. That’s our sudoku solver.

This works because the entire game relies on the board being logically coherent and sudokus always have at least one solution with 0 paradox. (which, if it did happen, would translate to a square having 0 possibility left, making the board unsolvable) In fact, thanks to sudoku’s coherent setting and rules, each of most sudokus has only one solution.

Now, what if we ran that solver on a completely empty board? Since our algorithm is looking for squares with one possibility, it’s probably not gonna work out. But let’s modify that behavior and make it look for the empty squares that have the least possibilities instead, then takes a random square from these and randomly picks one of its possibilities as the new value for the square. And just with that, our sudoku board is filling with random-but-coherent logic data.

That’s not it though. What do we do once the board is completely filled? Although watching the algorithm work can be very satisfying, a full board isn’t much fun. Stopping the algorithm before the board has reached completion would work but it would give out a grid with multiple solutions. Let’s say we want sudokus with only one unique solution, how do we make that happen?

This is actually the more difficult part and the one that has the longest processing time too. We need to remove random squares from the complete board, except that for every random square removed, we must check if the board still has only one solution, using the first sudoku solving algorithm. If the solving algorithm gets stuck (because none of the empty cases has only one possibility), we undo the last removing and we remove another square… And check again. This can be optimized by remembering what squares we failed to remove. But it’s still pretty slow.

Using such an algorithm until no more squares can be removed or before that, we can get a ton of sudokus of varying difficulties, each with their one unique solution! (which you can also save from when the board was complete)

And that’s our logic puzzle generator in two rather simple steps: the filling of the empty board and then the removing of random squares!

The reason I choose to write about sudoku generation here is that I thought it would be a great introduction for the Wave Function Collapse algorithm! (WFC for short)

Do you know about quantum mechanics? It’s the study of the very tiny elements that make up the world and their behaviors, which happen to be pretty mysterious still.

In quantum mechanics, there’s an event called the Wave Function Collapse. This event happens when an element with several simultaneous states (only possible in Quantum Mechanics™) suddenly appears to only have one state left when and after we observe it.

You may have heard of Schrodinger’s cat; it’s pretty much that, except there can be more than just two simultaneous states.

In our sudoku generation algorithm, we made a similar behavior! Empty squares were nothing less than elements with 9 possible states (or less if there’s already information on the board) and when we take a square and assign it one of its possibilities, we’re essentially collapsing its possibilities into just one.

And of course, the WFC algorithm is also akin to this behavior!

I didn’t really introduce that algorithm yet, so here it is: The WFC algorithm was made by МаГ (@ExUtumno) and it “generates bitmaps that are locally similar to the input bitmap”. Basically, you give it a bitmap and it will give you (or at least try to) a new bitmap that looks just like another version of the original bitmap.

The official page for the project is on github and here’s a few examples directly from that page. The input bitmap is on the left of the arrows and on the right are the generated results.

This algorithm has two versions and here I’m explaining the simpler one: the tiled version. This version actually does not use a bitmap but tiles and a map of those tiles. (bitmap version is quickly explained further down)

Here’s the essential of what this version of the algorithm does: (at least as I understand it)

• It takes as input a complete board of set tiles.
• It reads this board, registers the tiles and counts duplicates, so we give them more chances to appear during the generation later on.
• In ExUtumno’s algorithm, a symmetry system is used to reduce the number of different tiles some more. You can read about it on the WFC page, under ‘Tilemap Generation’, I won’t be using it here.
• The input board is read again and the algorithm makes a dictionary of neighbors: what tiles appear next to what tiles, on which sides.
• It creates an empty board much like our sudoku boards, with each square of the board being a dynamic array of all the possible tiles from the input board. At this point, every square of the board is all the different tiles at once.
• A random square of the board is set as a random tile.
• The neighboring tiles’ possibilities are reduced, according to their compatibility with their newly set neighbor, and then their neighbors’ tiles possibilities are reduced, etc until no more possibilities can be reduced.
• The last two steps are repeated until completion of the board, except each time we take a random square among the ones that have the fewest possibilities left.
• It builds the output visuals, mapped out by the now-complete board.

That’s all you need to know if you want to re-implement that algorithm yourself!

Since Pico-8 already has a tile system, I choose to use that with some handmade tiles. I simply made the tiles in the sprite-editor and built the input board in the map. As a counterpart, the tiles have a natural width of 8 pixels.

From there, the dictionary is built by the algorithm, as a construction of key-based tables, with each direction/side corresponding to a number from 0 to 3. The construction’s levels go ’tiles -> directions -> possible neighbors’.

The construction of the board happens exactly as previously explained, with tiles being used through their sprite id.

You can see the generation happen in the _draw function. For each square, we either draw the decided tile if it is decided, or we draw a tile indicating if there’s only a few possibilities left on that square or if there’s more.

One thing I didn’t really talk that much about yet is paradoxes. Paradoxes happen when set tiles contradict themselves and empty squares have no possibility left. With the WFC algorithm, this can happen but it very much depends on the way you control the neighbors’ possibilities. Let me explain.

One way to do it is that each time you set a value one an empty tile, you reduce the possibilities only on the immediate neighbors. This way is pretty fast but it’s also very prone to contradictions. One unaffected empty square, with all its possibilities, might be neighbor to two affected empty squares, with reduced possibilities; only there’s no tile that is capable to link any possibility from one side to any of the possibilities on the other side. And so we have a contradiction.

If we want to avoid contradictions, the best way is to go as far as we can from the tiles we set when removing possibilities. Every time we remove possibilities from a square, we look at the possible neighbor tiles for all the possibilities that are left, for each side. If those possible neighbor tiles are already all of the possibilities on the neighboring square, then we’re done. Otherwise, the neighboring square’s possibility should be reduced to this smaller pool of possibilities. And the cycle goes on until no more possibilities can be removed anywhere. With this method, the contradictions will be very rare but the generation will be very slow.

A compromise is a modification of the latter solution: when you remove possibilities from a square, you only check its neighbors if you removed enough possibilities. (at least 2) While still prone to the occasional contradictions, we’re already far from the first solution and it’ll be faster than the latter solution.

But in any case you will want to deal with contradictions when they do happen. The way to do that is not particularly graceful but it’s simple enough: make a history. Have as many previous versions of the board as you can and if you meet any contradiction, go back to the previous version. If the contradictions persist, go back to versions further back, until the contradictions stop happening.

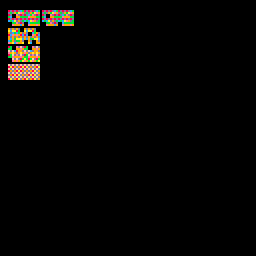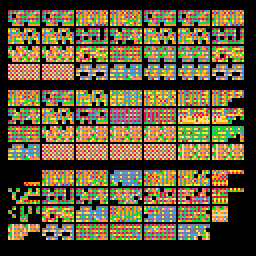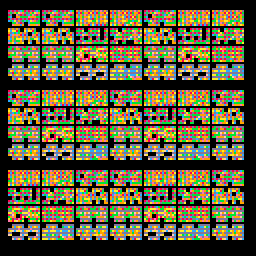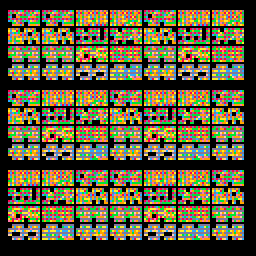
This WFC algorithm is very powerful and it can be used for more than just bitmaps! Here, I tried using it on music!

The very kind Chris Donnelly (@gruber_music) provided me with a Pico-8 track with only patterns of the same speed. I made an algorithm that could read the music data and chop it up in patterns that could be rearranged. Then I ran the WFC algorithm on the track, through these patterns. You can see the visualization of that above.

In the end the result was actually pretty boring, which is why I didn’t bother to upload it. (sorry :X) The generated output was just a continuous mix of the original and the interesting bits of the original track very rarely came up. Still, maybe if we fed such an algorithm with multiple tracks that have some patterns in common, I think we could get something pretty interesting!

But this WFC algorithm still has many other applications! Check these out!

• МаГ (@ExUtumno) also made a 3D voxel version. I’m pretty sure it’s unreleased as of now but they regularly post MagicaVoxel renders on Twitter!
• Oskar Stalberg (@OskSta) made another 3D version that uses polygonal tiles on a voxel grid. He also applied the algorithm to another creation of his that uses triangular tiles.
• Matt Rix (@MattRix) used the algorithm to create animations, by using time as a third dimension.
• Joseph Parker‘s (@jplur_) and Ryan Jones‘ (@poly_rhythm) game Proc Skate 2016 uses WFC to generate playable skateparks.
• Joseph Parker (@jplur_) implemented the algorithm as a Unity plugin.
• Martin O’Leary (@mewo2) used the algorithm on poetry.

As you can see, it’s a very versatile algorithm! The possibilities are huuuge! And yet…

This algorithm is tile-based. That is the one limitation that is essential to the algorithm working correctly. Even though it doesn’t have to be 2D tiles or even graphical tiles, it needs to come down as a tile system. And if what you want to generate isn’t naturally tile-based, you’ll have to accommodate.

That is for the tiled version of the WFC algorithm. I mentioned there was another version and that’s the overlapping version. This version is the one that uses an input bitmap. From this bitmap, the algorithm will extract as many tiles as possible, with 1-pixel offsets. Again, duplicates are counted and removed, but then the generation doesn’t go through neighbors, at least not as previously described. Instead, each pixel is its own empty square and the algorithm will attempt to find values for these squares that are coherent with the tiles extracted beforehand. These tiles are used as patterns that should be reproduced throughout the entire output bitmap regardless of tile alignment.

This second version is fairly more complicated to implement but it generates even more impressive results and does not require a tile system. However, I can only imagine that adapting it to anything else than bitmaps would be even more complicated and time-consuming, without even considering the process time of such generation. (or the required memory)

Aside from that, both version of the algorithm are only based on local logic. That means you can’t generate something like a sudoku for example, where the logic is global to the board and a tile can affect another tile at the other end of the board.

So the WFC algorithm is super powerful and you can adapt it to a lot of things – or rather adapt a lot of things to it – but it’s still not perfect for everything.

In the end, no algorithm can be perfect for everything. So why not just make ultra-specific algorithms?

In my experience, generations that do the best job are the ones you make with your precise goal in mind, like the one you’re seeing above. Think of the details and twists you want before starting and then work your way towards those.

The issue to take here is of course that you’d have to create a new algorithm for everything you want to generate. The pay-off is extremely good generated results.

 

Many procgen algorithms exist and almost all of them are about generating coherent results in some way, and some of them are particularly good! Yet, none are perfect and it’s good to know your options to choose the best for the situation. If you can’t think of any algorithm that can produce what you want to produce, maybe try and make your own and get some awesome results?

That’s it for those Doodle Insights, I hope you enjoyed reading them! If you have any questions or remarks, please do leave a comment here or on the Patreon post or tweet at me!

---

These Doodle Insights are brought to you by my awesome patrons on Patreon! Here are their names!

Ryan Malm, Goose Ninja, Joseph White, Brian Nicolucci, Thomas Wright, nanoplink, Cameron Brown, Chris McCluskey, Feliks Balzer, Wilhelm Murdoch, Andreas Bretteville, Joel Jorgensen, Corey O’Connor, Marty Kovach, Cole Smith, Giles Graham, Luke Davies, Tim and Alexandra Swast, Sasha Bilton, berkfrei, Jearl, Dave Hoffman, Jakub Wasilewski, Ian Fare, Brent Werness, Nick Hughes, Anne Le Clech, Nate Wiesel, Sean S. LeBlanc, Matt Hughes, Vorzam, Emerson Smith, C, Andrew Reist, vaporstack, Dżozef and Justin TerAvest

If you like what I do, the articles, the games, the gifs, please do consider supporting me on Patreon! You’ll get some exclusive content and you’d be helping me a lot! Thanks! 🙂

---

Thank you for reading and enjoy the coherant procgen!

TRASEVOL_DOG